【BSOJ2769】消息传递换根dp

2019-12-01

题目

H国的社会等级森严，除了国王之外，每个人均有且只有一个直接上级，当然国王没有上级。如果A是B的上级，B是C的上级，那么A就是C的上级。绝对不会出现这样的关系：A是B的上级，B也是A的上级。
　　最开始的时刻是0，你要做的就是用1单位的时间把一个消息告诉某一个人，让他们自行散布消息。在任意一个时间单位中，任何一个已经接到消息的人，都可以把消息告诉他的一个直接上级或者直接下属。
　　现在，你想知道：
　　1.到底需要多长时间，消息才能传遍整个H国的所有人？
　　2.要使消息在传递过程中消耗的时间最短，可供选择的人有那些？

$Solution$

这里主要介绍一个$O(n\log_2n)$的算法

虽然对于这道题$O(n^2\log_2n)$暴力枚举根已经可以$AC$了，但优化是无止境的

首先可以想出这道题对于一个确定的根的$dp$

再以任意点$root$为主根前提下

我们设$f_{i}$表示以$i$为根不计算根被传递到消息时间,把消息传到$i$为根的子树的最短时间

当$i$的子树均被计算完毕时

$\displaystyle{f_i=\max_{j\in son_i}}\{f_j+order_j\}$

其中$order_j$表示$j$是$i$的孩子中第$order_j$个选的，也就是他在$i$收到消息后第$order_j$个时间收到消息的

很容易想到贪心，我们让$f_j$值大的先传

单次复杂度$O(n\log_2n)$

但这样做需要枚举根，最终复杂度$O(n^2\log_2n)$

瓶颈在于什么,仔细思考我们会发现其实是我们确定了向“下”传的顺序，而因此很多子树的信息在不同的根下实际上是一样的

什么意思，我们看一下这幅图

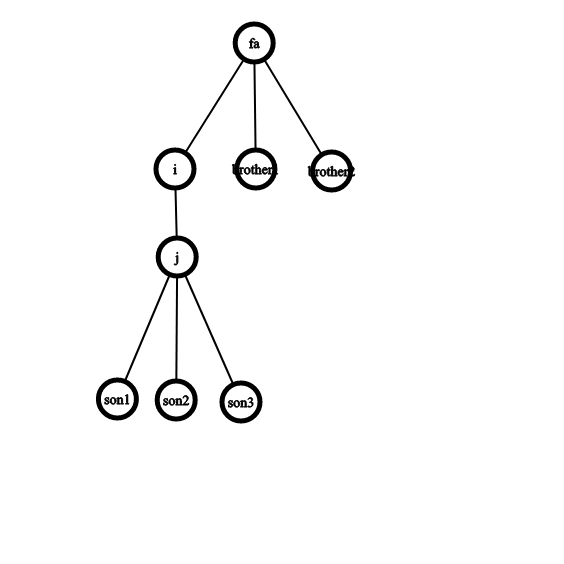
在$fa$,$i$,$brother1$,$brother2$作根的时候,以$j$为根的子树的形态没有一点改变

我们有没有办法一次计算这些信息呢

有的，那就是所谓的二次扫描与换根法

在李煜东的书里介绍了这个算法并给出了一个例题，但这个例题会更为复杂一些

我先重复一下这个算法流程

一次树形dp,求出每个点以$root$为根的子树中信息$down$
一次DFS求出每个点以$root$为根来自父亲的信息$up$,同时合并$up$和$down$

我们用这道题来看如何实现

对于$down$部分是类似的

设$down_{i}$表示不计算根被传递到消息时间,把消息传到$i$为根的子树的最短时间

我们在计算完了$i$的儿子$j$后来更新$i$

$\displaystyle{down_i=\max_{j\in son_i}}\{down_j+order_j\}$

$order$可以直接通过排序得到

inline void tree_dp(re int x){
	re int i,y,res=0;re vector<int> son;
	for(i=h[x];i;i=e[i].next){
		y=e[i].to;
		tree_dp(y);
		son.push_back(dpson[y]);
	}
	sort(son.begin(),son.end(),cmp);
	for(i=0;i<(int)son.size();++i)res=max(res,son[i]+i+1);
	dpson[x]=res;
}

而对于$up$部分

设$up_{i}$表示不计算根被传递到消息时间,把消息传到除了$i$为根的子树的节点的最短时间

可能很难理解，我们用一张图来展示

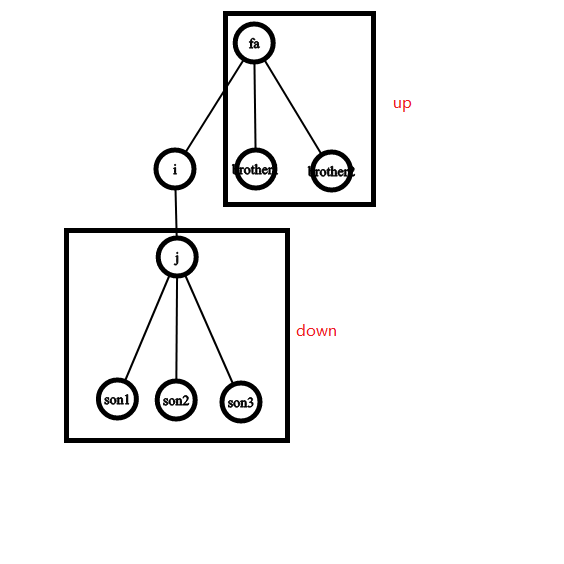
可以形象的理解为$down$对应的部分是在有根情况下向“下”的很多支子树,而$up$对应的部分是向“上”的那一支

我们在计算完了$j$的父亲$i$后来更新$j$

$\displaystyle{up_j=\max\{up_i+{order’}_{i}~,\max_{k\in son_i\vee k\ne j}}~\{down_k~+~order_{k}’\}~\}$

用这幅图理解一下,$up_j$保存的是来自父亲$i$的一支,其中包含了他父亲的父亲那一支$up_j$,也包含了$i$的父亲除了$i$的其他儿子支

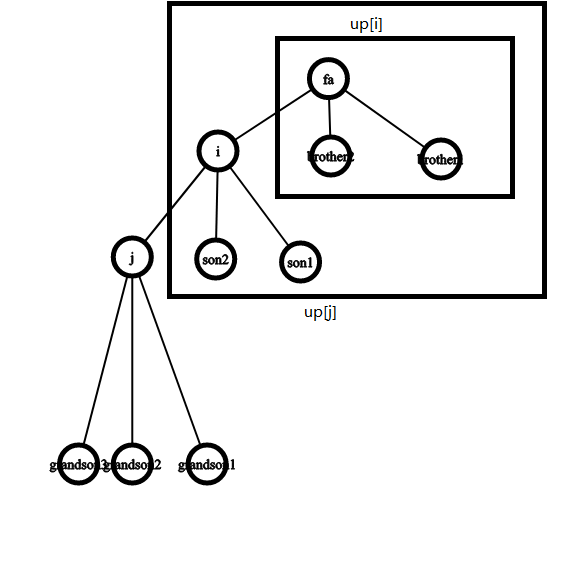
注意一下:为了处理方便，我们并不一开始显式去掉$i$的儿子$j$,而是吧$down_k$和$up_i$加进去排序,在需要求出$up_j$时我们二分查找$j$的位置,并把这个位置后面的位置的$order$值减一，因为我们在我们一开始的假设中，选$j$实际上是花了一个时间的，但实际并没有.实际操作上可以利用前缀和后缀$\max$来实现

1	inline void change_root(re int x){
2	re int i,y,pos;re vector<int> son;
3	for(i=h[x];i;i=e[i].next){y=e[i].to;son.push_back(dpson[y]);}if(fa[x])son.push_back(dpfa[x]);
4	sort(son.begin(),son.end(),cmp);
5	for(i=0;i<(int)son.size();++i)t[i]=son[i]+i+1;
6	*maxl=t[0];for(i=1;i<(int)son.size();++i)maxl[i]=max(maxl[i-1],t[i]);
7	maxr[son.size()-1]=t[son.size()-1];for(i=son.size()-2;i>=0;--i)maxr[i]=max(maxr[i+1],t[i]);
8	reverse(son.begin(),son.end());
9	for(i=h[x];i;i=e[i].next){
10	y=e[i].to;
11	pos=lower_bound(son.begin(),son.end(),dpson[y])-son.begin();pos=son.size()-pos-1;
12	if(!pos)dpfa[y]=max(0,maxr[1]-1);
13	else if(pos==(int)son.size()-1)dpfa[y]=max(0,maxl[pos-1]);
14	dpfa[y]=max(maxl[pos-1],maxr[pos+1]-1);
15	}
16	dp[x]=maxl[son.size()-1];for(i=h[x];i;i=e[i].next){y=e[i].to;change_root(y);}
17	}

其他细节比如边界什么的需要做了才知道

#include<bits/stdc++.h>
#define N 200005
#define re register
#define INF 0x3f3f3f3f
using namespace std;
struct read{
	char buf[1<<25],*opt;
	read():opt(buf){buf[fread(buf,1,sizeof buf,stdin)]=0;}
	template<typename _int>
	operator _int(){
		_int res=0,flag=1;
		while(*opt<48&&*opt!='-')++opt;
		if(*opt=='-'){flag=-1;++opt;}
		while(*opt>32)res=(res<<1)+(res<<3)+(*opt++)-48;
		return res*flag;
	}
}it;
inline char cmp(re int x,re int y){return y<x;}
struct Edge{int to,next;}e[N<<1];
int n,cnt,h[N],t[N],dpson[N],dpfa[N],maxl[N],maxr[N],fa[N],dp[N],ans=INF,Ans[N];
inline void AddEdge(re int x,re int y){e[++cnt]=(Edge){y,h[x]};h[x]=cnt;}
inline void tree_dp(re int x){
	re int i,y,res=0;re vector<int> son;
	for(i=h[x];i;i=e[i].next){
		y=e[i].to;
		tree_dp(y);
		son.push_back(dpson[y]);
	}
	sort(son.begin(),son.end(),cmp);
	for(i=0;i<(int)son.size();++i)res=max(res,son[i]+i+1);
	dpson[x]=res;
}
inline void change_root(re int x){
	re int i,y,pos;re vector<int> son;
	for(i=h[x];i;i=e[i].next){y=e[i].to;son.push_back(dpson[y]);}if(fa[x])son.push_back(dpfa[x]);
	sort(son.begin(),son.end(),cmp);
	for(i=0;i<(int)son.size();++i)t[i]=son[i]+i+1;
	*maxl=t[0];for(i=1;i<(int)son.size();++i)maxl[i]=max(maxl[i-1],t[i]);
	maxr[son.size()-1]=t[son.size()-1];for(i=son.size()-2;i>=0;--i)maxr[i]=max(maxr[i+1],t[i]);
	reverse(son.begin(),son.end());
	for(i=h[x];i;i=e[i].next){
		y=e[i].to;
		pos=lower_bound(son.begin(),son.end(),dpson[y])-son.begin();pos=son.size()-pos-1;
		if(!pos)dpfa[y]=max(0,maxr[1]-1);
		else if(pos==(int)son.size()-1)dpfa[y]=max(0,maxl[pos-1]);
		else dpfa[y]=max(maxl[pos-1],maxr[pos+1]-1); 
	}
	dp[x]=maxl[son.size()-1];for(i=h[x];i;i=e[i].next){y=e[i].to;change_root(y);} 
}
int main(void){
	n=it;
	re int i;
	for(i=2;i<=n;++i){fa[i]=it;AddEdge(fa[i],i);}
	tree_dp(1);change_root(1);
	for(i=1;i<=n;++i)if(dp[i]<ans){ans=dp[i];Ans[*Ans=1]=i;}else if(ans==dp[i])Ans[++*Ans]=i;
	printf("%d\n",ans+1);
	for(i=1;i<=*Ans;++i)printf("%d ",Ans[i]);
	return 0;
}