题目描述
JOI村有一片荒地,上面竖着N个稻草人,村民们每年多次在稻草人们的周围举行祭典。
有一次,JOI村的村长听到了稻草人们的启示,计划在荒地中开垦一片田地。和启示中的一样,田地需要满足以下条件:
田地的形状是边平行于坐标轴的长方形;
左下角和右上角各有一个稻草人;
田地的内部(不包括边界)没有稻草人。
给出每个稻草人的坐标,请你求出有多少遵从启示的田地的个数
简述 求$n$个点组成的内部不含其它点的矩形有多少
Solution
为什么要专门记录这个简单的$CDQ$分治+单调栈简单题呢,那是因为这道题脱离了$CDQ$分治的模板,转更深刻的探究$CDQ$分治解决的问题本质
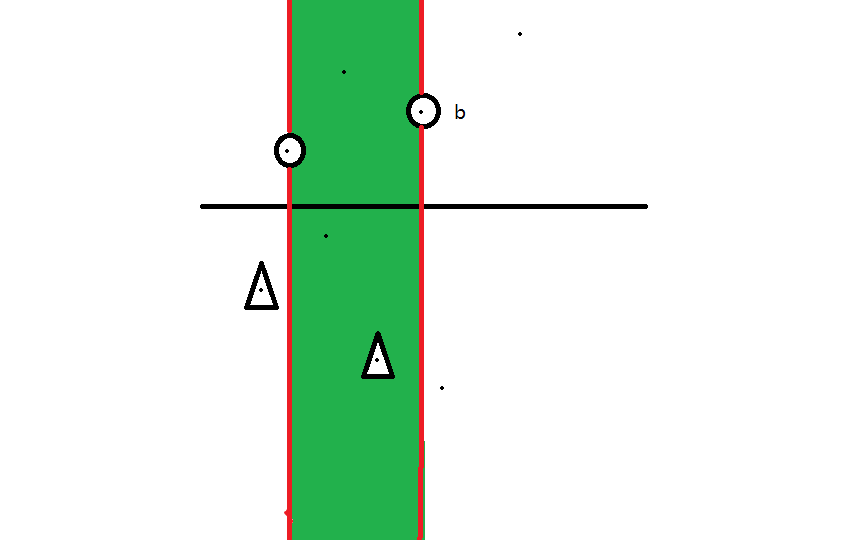
首先这道题找矩形,就要找其左下角及右上角
我们把被处在右上角的点$b$与左下角的点$a$形成有效矩形成称为$b$控制$a$
可理解为,处在左下位置的点会对右上位置的点造成贡献,被控制
我们把点按$y$轴排序
按$y$来划分上下
上下以$x$来归并排序(结果就是,$[ql,mid]$的$y$都比$[mid+1,qr]$的$y$要小,但区间内有且仅有$x$有序)
如图,$[ql,mid]$为上面,$[mid+1,qr]$为下面
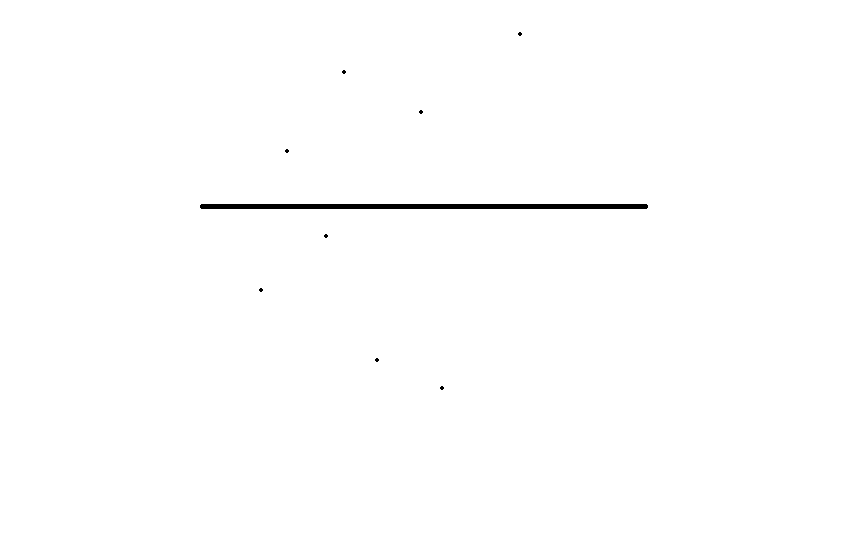
因此$a$来自下方,$b$来自上方
$Ans_b$=(在$b$左侧可以成为左下角的$a$-被$b$左边的管并且不会被$b$管的$a$)
对在$b$左侧可以成左下角的$a$
现在证明:如果$a$是满足条件的,则在$a$右上侧的$a’$就是无效的
分两种情况
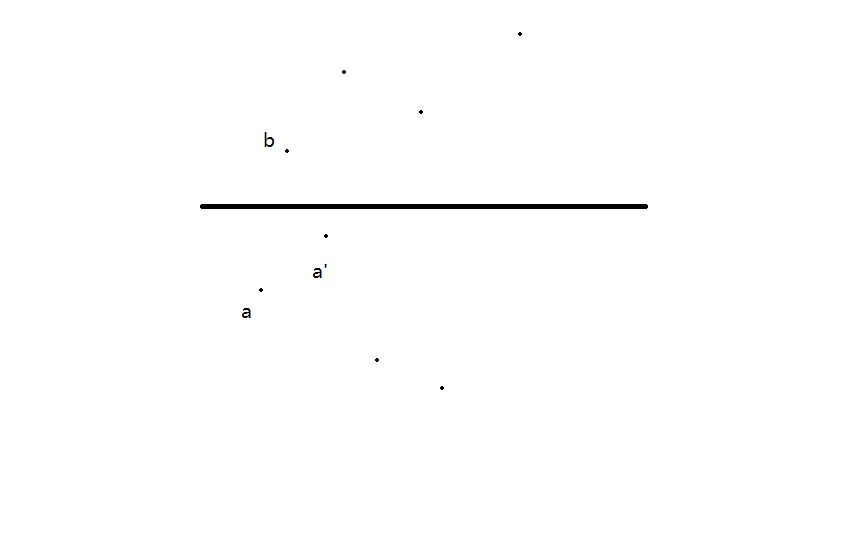
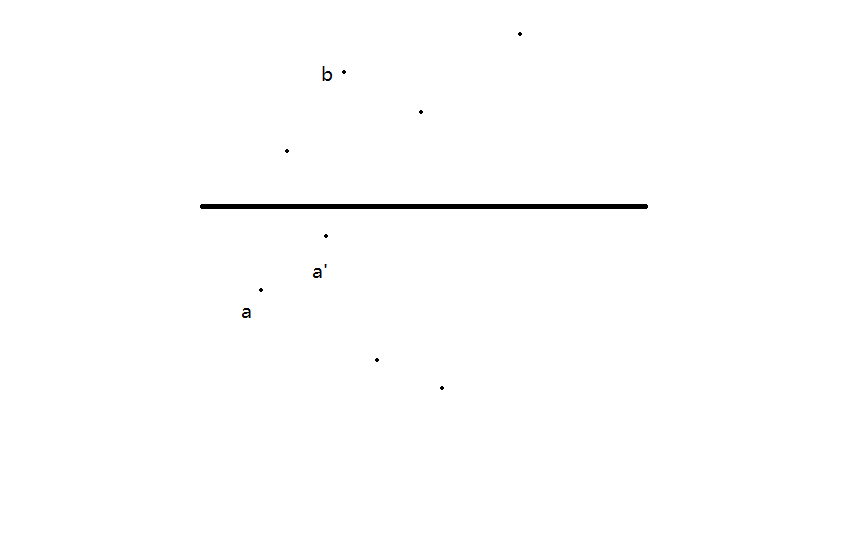
因此对$a$我们维护一个$y$值单调递减的单调栈
每次维护$x<b_x$的单调栈即可
1 | for(;q[j].x<q[i].x&&j<=mid;++j){//下,保存的是所有可以成为左下角的点 |
2 | while(topmax&&q[j].y>q[stmax[topmax]].y)--topmax; |
3 | stmax[++topmax]=j; |
4 | } |
被$b$左边的管并且不会被$b$管的$a$
现在证明:在$b$左下侧的$b’$是不会影响$b$管辖范围的
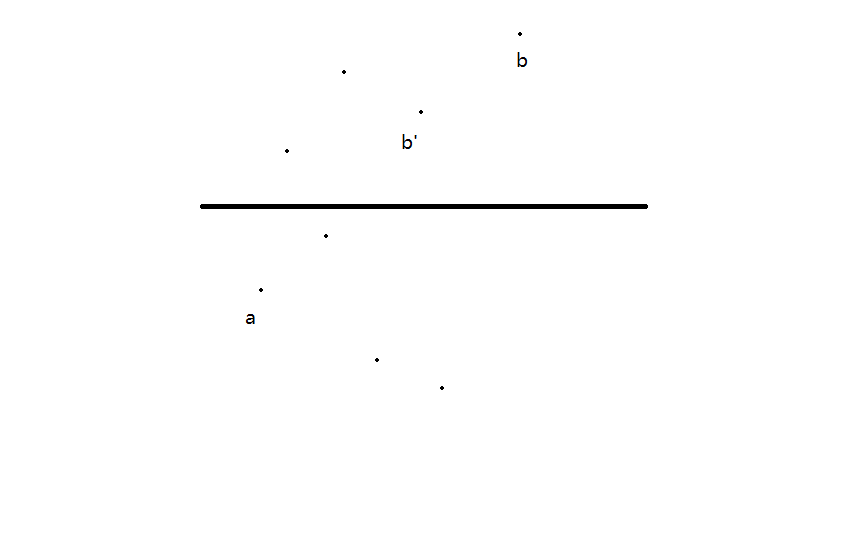
因此对$b$我们维护一个$y$值单调递增的单调栈
每一次
$Ans_b$=(在$b$左侧可以成为左下角的$a$-被$b$左边的管并且不会被$b$管的$a$)
=$topmax-b$的单调栈的前栈顶管辖的$a$个数
实现时用二分即可找到前栈顶管辖的最后一个$a$位置减掉即可
1 | |
2 | inline int Find(void){ |
3 | re int l=1,r=topmax,mid,ans=0; |
4 | while(l<=r){ |
5 | mid=(l+r)>>1; |
6 | if(q[stmax[mid]].x<q[stmin[topmin-1]].x){ans=mid;l=mid+1;} |
7 | else r=mid-1; |
8 | } |
9 | return ans; |
10 | } |
11 | inline void CDQ(re int ql,re int qr){ |
12 | re int i,j,l,r,t,mid=(ql+qr)>>1; |
13 | if(ql==qr)return ; |
14 | CDQ(ql,mid);CDQ(mid+1,qr); |
15 | j=ql;topmin=topmax=0; |
16 | for(i=mid+1;i<=qr;++i){//上,保存的是所有可以影响之后右上角点的(左下角点的个数)的点 |
17 | while(topmin&&q[i].y<q[stmin[topmin]].y)--topmin; |
18 | stmin[++topmin]=i; |
19 | for(;q[j].x<q[i].x&&j<=mid;++j){//下,保存的是所有可以成为左下角的点 |
20 | while(topmax&&q[j].y>q[stmax[topmax]].y)--topmax; |
21 | stmax[++topmax]=j; |
22 | } |
23 | ans+=topmax-Find(); |
24 | } |
25 | l=t=ql;r=mid+1; |
26 | while(l<=mid&&r<=qr){ |
27 | if(q[l].x<q[r].x)tmp[t++]=q[l++]; |
28 | else tmp[t++]=q[r++]; |
29 | } |
30 | while(l<=mid)tmp[t++]=q[l++]; |
31 | while(r<=qr)tmp[t++]=q[r++]; |
32 | for(i=ql;i<=qr;++i)q[i]=tmp[i]; |
33 | } |
放一个示意图(一定要手推)