【前置知识】

组合数公式($n\in N$):$C_n^m$=$\frac{n!}{(n-m)!\cdot m!}$

拓展（$n\in R$）:$C_n^m$=$\frac{\prod_{i=n-m+1}^n{}i}{m!}$

二项式定理:$(a+b)^n = \sum_{i=0}^{n} C_n^i a^{n-i} b^i (n>0)$

拓展:$(a+b)^{-n} = \sum_{i=0}^{-n} C_{-n}^i a^{n-i} b^i(n>0)$

一.普通生成函数

【定义】

假设你有一个函数$f(n)$

这个函数不好求(卷积)，尤其是在它的定义很复杂时

这时我们构造$f$的生成函数$g^{f}(x)=\sum_{i=0}^{∞}f(i) * x^i$

一个很重要的点：为保证这个求和收敛需要$-1 < x < 1$，但这个$x$是没有实际意义的，在后面可以看出，它是用来反解系数的。

【应用】

例题:_$gyh$要买东西，他要买$3$的倍数个$a$,至少$4$个$b$求买了$n$个字母的情况数_

解答:首先确定这里的方案数是组合。

定义$f(n)$表示买了$n$个字母的情况数,$h_i(n)$表示第$i$种字母，选$n$个可取性

这里再定义$g^{f}(x)=\sum_{i=0}^{∞}f(i)\cdot x^i=g_a(x)\cdot g_b(x)$

对$h_a:(1,0,0,1,0,0,1)->g_a(x)=\frac{1}{(1-x)^3}$

对$h_b:(0,0,0,0,1,1,1)->g_b(x)=\frac{x^4}{1-x}$

因此$g^f(x)=\frac{x^4}{(1-x)^4}$

求出其第$n$项即可

【例题】

【一】$BSOJ4763$:模板

偶数 $(1,0,1,0,1,0)->g_1(x)=\frac{1}{1-x^2}$

$3$的倍数 $(1,0,0,1,0,0)->g_2(x)=\frac{1}{1-x^3}$

$4$的倍数 $(1,0,0,0,1,0)->g_3(x)=\frac{1}{1-x^4}$

0或1个$(1,1,0,0,0,0)->g_4(x)=\frac{1}{1-x}-\frac{x^2}{1-x} =\frac{1-x^2}{1-x}=1+x$

不超过一个(同上)$(1,1,0,0,0,0)->g_5(x)=\frac{1-x^2}{1-x}=1+x$

0,1或2个$(1,1,1,0,0,0)->g_6(x)=\frac{1}{1-x}-\frac{x^3}{1-x} =\frac{1-x^3}{1-x}$

0,1,2或3个$(1,1,1,1,0,0)->g_7(x)=\frac{1}{1-x}-\frac{x^4}{1-x} =\frac{1-x^4}{1-x}$

奇数 $(0,1,0,1,0,1)->g_8(x)=\frac{x}{1-x^2}$

累乘即得$g^f(x)=\frac{x}{(1-x)^4}=(1-x)^{-4} * x$

$=x\cdot\sum_{i=0}^∞C_{4+i-1}^i\cdot x^i$

$=x\cdot\sum_{i=0}^∞C_{3+i}^3\cdot x^i$

$=\sum_{i=0}^∞C_{3+i}^3\cdot x^{i+1}$

$=\sum_{i=1}^∞C_{2+i}^3\cdot x^i$

则$f(n)=C_{2+n}^3$

$Code$

【二】

首先我们要求卡特兰数

$C_n=\sum_{i=0}^{n-1}C_i\cdot C_{n-i-1}$

定义生成函数$g^C(x)=\sum_{i=0}^{∞}C_i\cdot x^i$

所以有$g^C(x)=x\cdot g^C(x)^2+1$(卷积性定义可得)

解得$g^C(x)=\frac{1-\sqrt{1-4x}}{2x}$

然后就

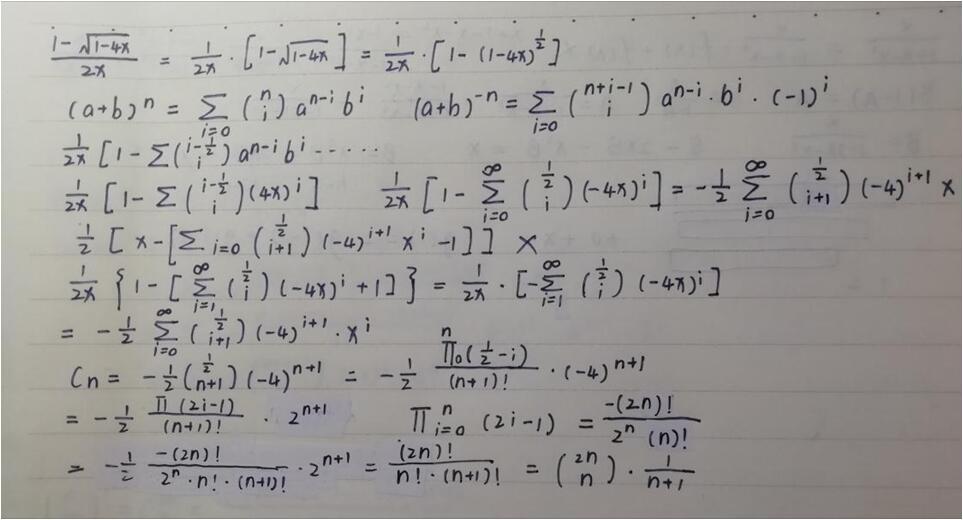
【三】

【练习】

$1.$$BSOJ4705$

【简述】给你$n$个正整数$a_1-a_n$

求对选一个或两个或三个的和可能取值的方案数

【题解】设$Ans(x)$为斧头的生成函数，其中第$x^i$项的系数为价值为$i$的斧头个数

$A(x)$表示同一个斧头重复一次价值为$x$的斧头个数

$B(x)$表示同一个斧头重复二次价值为$x$的斧头个数

$C(x)$表示同一个斧头重复三次价值为$x$的斧头个数

对$A^2(x)$，会产生$(x_i,x_i)$同一把斧头的贡献，所以定义$B(x)$为同一个斧头重复两次的方案数，那么$A^2(x)-B(x)$就是两把斧头时真正的贡献，又因为与顺序无关，所以还要除以$2$

然后$A^3(x)$的话，可能会有一把斧头重复两次或三次，如果重复两次，那么就是$(x_i,x_i,y_i),(x_i,y_i,x_i),(y_i,x_i,x_i)$，就是$3A(x)B(x)$，但是减去这个的话又会把$(x_i,x_i,x_i)$的情况多减去两次，所以定义$C(x)$为同一把斧头重复三次的生成函数，于是还要加上$2C(x)$，然后无关顺序的话还要除掉$3!=6$

综上，最终的答案的生成函数为$Ans(x)=A(x)+\frac{A^2(x)-B(x)}{2}+\frac{A^3(x)-3A(x)B(x)+2C(x)}{6}$

$2.$$BSOJ4370$

【题意】给你$n$个正整数$a_1-a_n$

每次随机选出三个数。问这三个数能组成三角形的概率为多大？

【题解】暂空