简述
后缀数组是一种后缀数据结构,记录一个字符串后缀按字典序排序的结果$SA_i$以及其与前后串$LCP$(最长公共前缀)$Height_i$
求法
定义
- $SA_i$表示$\text{Suff}_i$的排名
- $rank_i$表示排名为$i$的后缀是$\text{Suff}_{rank_i}$
- $Height_i$表示$LCP\{\text{Suff}_{SA_i},\text{Suff}_{SA_{i-1}}\}$
思想(基排)
从低位向高位排序,但直接做是$O(n^2)$的
瓶颈在于比较每次都与长度相关,考虑利用$rank$本身的表示的大小意义
考虑倍增
假设长度为$2^0$到$2^{k-1}$的排名已经求出
对于$i$开始长度为$2^k$的串,我们只需要比较$i$开始长度为$2^{k-1}$的串(第一关键字),$i+2^{k-1}$开始长度为$2^{k-1}$的串(第二关键字)
举个栗子:
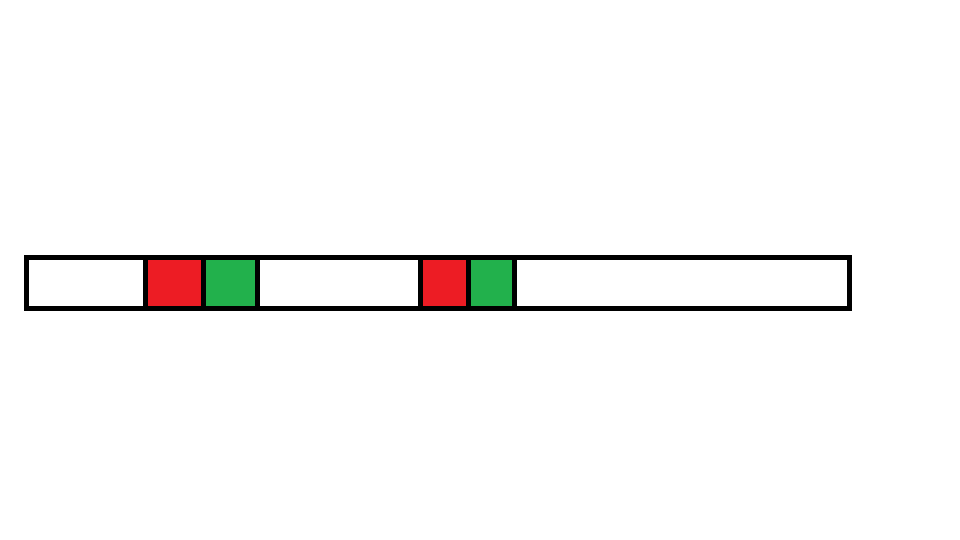
比较前后两端就等于先排绿再排红
步骤

- 1.对每一位($k=0$)排序
1 | for(i=1;i<=n;++i)++sum[x[i]=s[i]]; |
2 | for(i=1;i<=m;++i)sum[i]+=sum[i-1]; |
3 | for(i=n;i;--i)SA[sum[x[i]]--]=i; |
- 2.利用$2^{k-1}$$rank$双关键字排序
理解一下在$swap$之前$y_i$表示第二关键字排名为$i$的起始位置
$fisrt_i$表示第二关键字排名为$i$的第一关键字的排名
1 | for(j=p=1;p<n;m=p,j<<=1){ |
2 | for(i=n-j+1,p=0;i<=n;++i)y[++p]=i; |
3 | for(i=1;i<=n;++i)if(SA[i]-j>0)y[++p]=SA[i]-j; |
4 | for(i=1;i<=n;++i)first[i]=x[y[i]]; |
5 | memset(sum,0,(m+1)<<2); |
6 | for(i=1;i<=n;++i)++sum[first[i]]; |
7 | for(i=1;i<=m;++i)sum[i]+=sum[i-1]; |
8 | for(i=n;i;--i)SA[sum[first[i]]--]=y[i]; |
9 | std::swap(x,y);x[SA[1]]=1; |
10 | for(i=2,p=1;i<=n;++i){ |
11 | if((y[SA[i-1]]!=y[SA[i]])||(y[SA[i-1]+j]!=y[SA[i]+j]))++p; |
12 | x[SA[i]]=p; |
13 | } |
14 | } |
- 3.利用性质$Height_{rank_i}\ge Height_{rank_{i-1}}-1$
1 | for(i=1;i<=n;++i){ |
2 | if(rank[i]>>1){j=SA[rank[i]-1];while(s[i+res]==s[j+res])++res;height[rank[i]]=res;if(res>0)--res;} |
3 | else height[rank[i]]=0; |
4 | } |
经典运用
后缀$LCP$
$LCP\{Suff_i , Suff_j\}$=$\displaystyle{\min_{k=rank_i+1}^{rank_j}Suff_k}$
【证明】我们可以知道$LCP$尽量长的后缀排名会越接近,因此求两两后缀的$LCP$一定是他们临近排名间被传递公用的部分
最长回文
首先原串变为$S+O+S^{-1}$
对奇数串
设中间点为$i$
若红与绿等长$l$则因为对称性回文长为$2l+1$
即$ans=2LCP(i,n-i)+1$
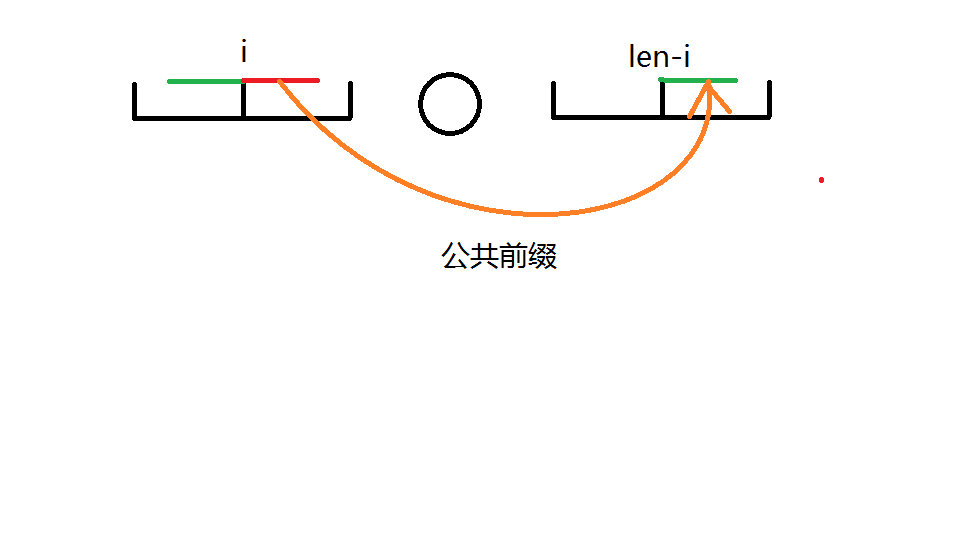
类似的偶数串
设中点后点为$i$
$ans=2LCP(i,n-i+1)$
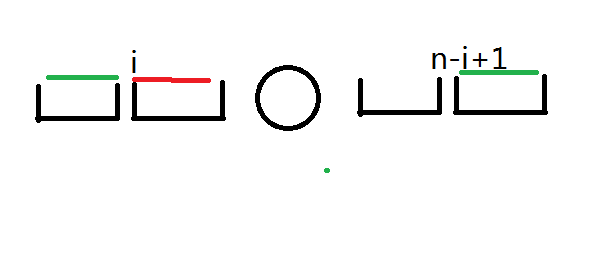
最长公共子串
利用子串就是后缀的前缀,把他们拼起来
最长的前缀一定出现在连续(排名)两个后缀之间
判定一下位置即可
- 最长公共子串(n串)$BSOJ2815$
把$n$个串拼起来,二分长度
按排名看是否存在连续$n$个后缀(注意$belong$)前缀那么长
1 | inline char Check(re int mid){ |
2 | ++sign;re int i,res=0; |
3 | for(i=1;i<=len;++i){ |
4 | if(height[i]<mid)++sign,res=0; |
5 | if(col[belong[SA[i]]]^sign)col[belong[SA[i]]]=sign,++res; |
6 | if(res==n)return 1; |
7 | } |
8 | return 0; |
9 | } |
不同子串个数
结论$\displaystyle{ans=\sum_{i=1}^n}n-SA_i+1-height$
$Suff_{SA_i}$会形成$n-SA_i+1$个前缀,其中$Height_i$个与前面相同
| 题目 | 做法 | 简述 |
|---|---|---|
| $1355$ | 后缀数组+RMQ | |
| $1590$ | 后缀数组 | |
| $1856$ | 虚树+后缀自动机or后缀数组+单调栈 | |
| $2144$ | 后缀数组+差分+二分 | |
| $2230$ | 后缀数组 | |
| $2801$ | 后缀数组+子串计数+容斥 | |
| $2815$ | 后缀数组+二分+最长公共子串 | |
| $2954$ | KMPor后缀数组 | |
| $3166$ | 后缀数组 | |
| $3167$ | 后缀数组 | |
| $3236$ | 后缀数组+待修改 or 后缀自动机 | |
| $3296$ | 后缀数组 | |
| $3403$ | 后缀数组+最小表示法 | |
| $3563$ | 后缀数组+Height+二分 | |
| $3579$ | 后缀数组+Manachar | |
| $3580$ | 后缀数组 | |
| $3582$ | 后缀数组 | |
| $3584$ | 后缀数组 | |
| $3744$ | 后缀数组 | |
| $4037$ | 后缀自动机+后缀数组 | |
| $5209$ | 后缀数组 |